우리가 신호를 처리하는, 그리고 시스템의 반응을 분석하는 방법은 특정 신호의 특성과 속성에 크게 의존합니다. 따라서 우리는 신호를 몇개의 그룹으로 묶어야 할 필요가 생겼고, 각 그룹 별로 신호를 다루는 방법을 다르게 적용해야만 합니다.
Multichannel and Multidimensional Signals
앞에서 조금 살펴보았지만, 우리는 신호를 한 개 혹은 그 이상의 독립 변수를 입력으로 갖는 함수로 묘사할 수 있다고 하였습니다. 다채널 신호(Multichannel Signals)는 같은 독립변수의 입력에 대해 여러 개의 출력 값을 갖는 신호를 말합니다. 이를테면, 센서 여러 개로 측정해야 하는 뇌전도, 심전도 혹은 지진파 등이 있습니다. 우리는 다채널 신호를 다음과 같이 벡터 형태로 나타낼 수 있습니다.
그렇다면 다차원 신호(Multidimensional Signals) 는 무엇일까요? 바로 입력이 되는 독립변수의 개수가 2개 이상일 때를 말합니다. 대표적인 것이 이미지가 있을 수 있겠습니다. 그렇다면, 다채널이면서 다차원인 신호도 있겠죠? 가장 우리에게 와닿는 예시는 바로 TV 화면입니다. TV 화면 신호를 수식으로 정의해보면 다음과 같을 것 입니다.
는 시간 t일 때 좌표 (x,y) 에 위치하는 픽셀의 값이고, r,g,b 세 값을 갖고 있을 것이므로 벡터로 표현됩니다.
Continuous-Time Versus Discrete-Time Signals
신호를 분류하는 또 다른 기준으로, 입력 파라미터인 시간이 연속적인지 불연속적인지 를 둘 수 있습니다.
연속-시간 신호는 아날로그 신호라고도 하며, 시간이 의 실수 모든 값을 가질 수 있을 때를 말합니다.
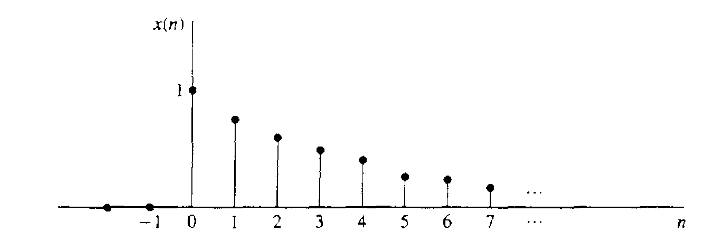
반면, 이산-시간 신호는 시간 자리에 인덱스 n 을 넣고, 이산적인 값을 파라미터로 갖는 신호입니다. 표기는 다음과 같이 할 수 있습니다.
이산-시간 신호는 다음 두 가지 방법으로 얻을 수 있습니다.
- 샘플링 (Sampling) : 아날로그 신호에서 특정 시간마다 그 때의 값을 선택하여 신호를 재구성하는 방법입니다. 샘플링에 대해서는 추후에 자세히 다루도록 하겠습니다.
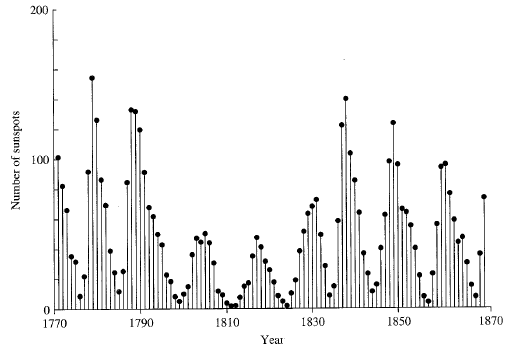
- 누적 (Accumulation) : 어떤 주기마다 일어나는 값들을 축적시켜서 신호를 재구성하는 것입니다. 도로를 지나가는 자동차의 수를 시간별로 나타내는 신호가 있다고 생각해봅시다. 이를 이산-시간 신호로 바꾸기 위해서, 매 시간마다 한 시간동안 도로를 이용했던 자동차의 수를 세어서 기록할 수 있겠죠. 다음은 매년 관측된 흑점의 수를 이산-시간 신호로 나타낸 그래프입니다.
Continuous-Valued Versus Discrete-Valued Signals
연속-시간 신호와 이산-시간 신호 모두 값에 대해서는 연속적일 수 있고, 불연속적일 수 있습니다. 만약 신호가 유한한 혹은 무한한 범위 내에서 가능한 모든 값을 가질 수 있다면, 이를 연속-값 신호(continuous-valued) 라고 부릅니다. 반면 신호가 유한한 개수의 원소를 갖는 집합으로부터 값을 갖는다면 이를 이산-값 신호(discrete-valued) 라고 부릅니다. 그리고 연속-값 신호로부터 이산-값 신호를 얻는 방법으로는 양자화(Quantization) 이 있습니다. 간단한 양자화 방법으로 정해놓은 유효숫자까지 반올림 혹은 버림을 사용합니다. 이 역시 추후에 자세히 다뤄보도록 하겠습니다.
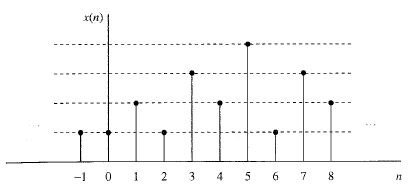
만약 신호가 시간과 값에 대해 모두 이산적이라면, 이런 신호를 우리는 디지털 신호라고 부릅니다. 다음 그림은 디지털 신호의 예시를 그려놓은 그래프입니다.
Deterministic Versus Random Signals
신호를 수학적으로 분석하거나 처리하려면 신호에 대한 수학적 묘사가 가능해야합니다. 이런 수학적인 묘사를 신호 모델(Signal model) 이라고 부르고, 이는 신호들을 또 다르게 분류하는 데에 매우 중요한 역할을 합니다.
어떤 신호가 수학 공식, 데이터 테이블, 혹은 잘 정의된 룰에 기반하여 유일하게 묘사될 수 있다면 결정적(Deterministic) 이라고 합니다. 이런 특성을 ‘결정적’ 이라고 한 이유는, 신호가 과거, 현재, 그리고 미래에 갖는 값들을 확실하게 추정할 수 있기 때문입니다. 즉, 불확실성이 없다 는 것입니다.
하지만 우리가 실제로 만나는 대부분의 신호들은 완벽하게 수학 공식으로 묘사할 수 없고, 따라서 신호의 과거와 현재 값을 안다고 해서 미래의 값을 정확하게 추정할 수 없습니다. 이런 신호의 특성을 우리는 랜덤(Random) 이라고 합니다. 확률 이론과 확률 과정론(Theory of probability and stochastic processes)에서는 이런 랜덤 신호에 대한 이론적 분석을 다룹니다.
실제 세계에서는 신호를 결정적 혹은 랜덤하다고 명확하게 나눌 수 없습니다. 심지어 분석하고자 하는 신호가 두 성질을 모두 갖는다고 볼 때 더 좋은 결과를 가져다 주고는 합니다. 이에 대해서는 역시 추후에 자세히 알아보도록 합시다.